

In Part 1, we looked at how a fixture manipulates its distribution of light. Because the distribution describes how light spreads out from a source, for Part 2, it seems logical to explore how this spreading out directly influences the loss of illuminance measured at further distances. Conceptually, this is easy enough to understand when considering light as a quantity that thins out as it expands, like an inflating balloon. More obviously, this can be observed by noting that Illumination drops as the distance from a light source increases, and Illumination increases as the light is moved closer.
The rate of expansion, and consequently the rate at which illumination decreases is referred to as the Falloff Rate. Many of us were taught that the falloff rate for a light source is absolute and follows the Inverse-Square Law of decay. As such, understanding this Law can be a helpful tool on set. However, while the Law is scientifically sound in reference to a “point source,” implementing the law on set to calculate illuminance at a distance will often produce results that are inconsistent with measurements. Nevertheless, it is important that we review the Inverse-Square Law before attempting to understand the limitations of its applications.
The easiest way to understand the Inverse-Square Law is usually to apply the rule that if you double the distance, you take one-quarter of the original intensity.


Figure 1
The standard depiction of the Inverse-Square Law at work
This is where the name of the law comes from –
Inverse: Taking the reciprocal of the distance
(2 feet becomes ½)
Squared: Raising that reciprocal to the power of 2
(2 feet becomes ½² = ¼)


However, while this law is absolutely true, the variables at play will often produce results that prove problematic when trying to use this formula on set.
You are shooting a lower-light scene with an actor with a very dark skin tone.
The DP is shooting at ISO 800 with a wide open lens set to f4.
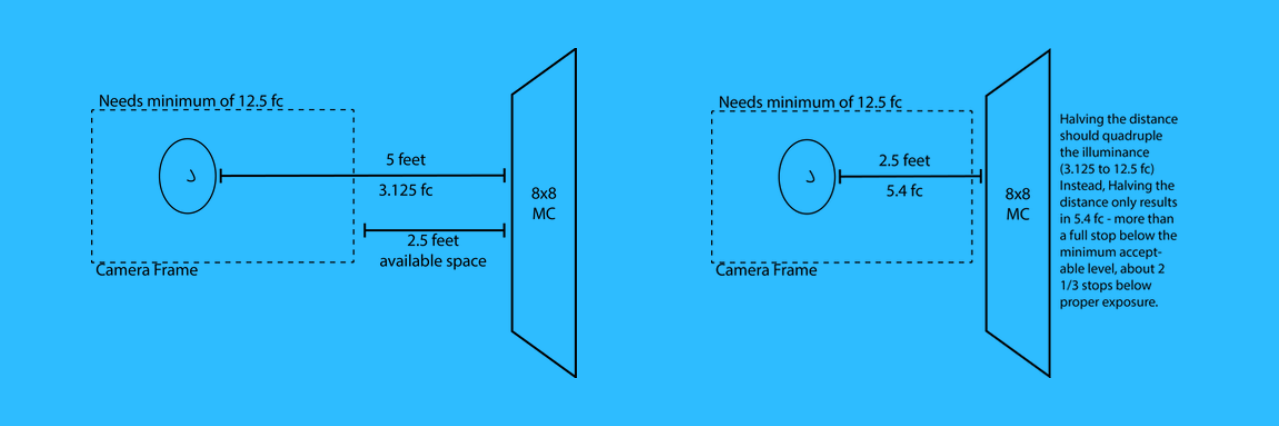
Your key light is currently shooting through an 8×8 frame of Magic Cloth™ at 5 feet away, the illuminance at the subject is measuring 3.125 footcandles.
To match the mood of the scene and due to the skin tone of the actor, the DP cannot have the actor more than 1 stop underexposed.
Proper exposure requires 25 fc meaning the least acceptable amount of light is 12.5 fc (1 stop under 25 fc).
Using the Inverse-Square Law principle, you believe that if you were to move the light and the 8×8 to the edge of the camera frame, you would be halving the distance (2.5 ft away), and multiplying the illuminance by 4x. This would give you the 12.5 fc minimum that you need. However, when you halve the distance, you’re only reading 5.4 fc: about 2⅓ stops below proper exposure! Why did this happen?

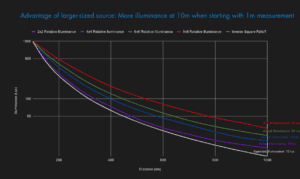

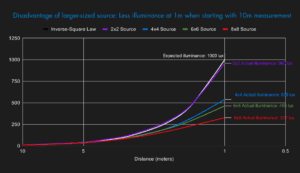

The graphs above highlight one of the problems with using the Inverse-Square Law. As was said earlier, the Law applies to the expansion of light from a point source. A point source expands isotropically (equally in all directions) and therefore has a consistent rate. However, in the scenario and graphs above, the source is actually made up of billions of point sources, all with equal intensity and arranged along a plane. At a far enough distance (about 5x the largest dimension) this collection of point sources will have combined to appear as one source and will begin to falloff at the rate of the Inverse-Square Law. In the meantime, before that distance is reached, the falloff rate will be dynamically changing. The above scenarios nicely demonstrate how the distance, relative to the size/shape of a collection of point sources, all equal in intensity can skew the law’s expectations. The greater number of point source’s in an area, the more their combined distribution patterns will merge and influence the illumination level at any given distance.
While distance, relative to size is one way that a fixture can influence the distribution pattern, as we observed in Part 1, many fixtures employ the use of lenses or reflectors as a means of redistributing illuminance, also altering the distribution pattern. For more optically pure fixtures, his can result in “virtual origin points” that do follow the law — but from a different origin point. While other, less optically pure fixtures, like many fresnels or PARs, will have a number of variables altering the falloff rate. In some cases, this produces a greater concentration of light but a falloff rate that is greater than the Inverse-Square Law! In any case, this reveals an important lesson to remember:
The Distribution Pattern
directly influences the Falloff Rate
A falloff rate that does not follow the Inverse-Square Law for calculation can be represented by changing the exponential power in the equation. Calculating an exponent greater than 2 means that the fixture will lose illuminance sooner over distance, whereas an exponent that is less than 2 indicates the fixture illuminance will decrease more gradually over distance.
>2 = more drastic falloff
<2 = more gradual falloff
In all cases, the exponent is actually dynamic: changing as the measured distances change. At a certain distance, this change will begin to level-out to an exponent around 2. However, with many of the fixtures that we use, that leveling-out does not occur within the common distances that the fixtures are used at.
A simple way to understand this exponent is by comparing it to the speed of a car. If the speed is fixed, it is easy to calculate what time a car will reach any distance when given the starting time and the speed. However, a dynamic exponent is equivalent to the speed of a car that is decelerating to a fixed speed. If the car is decelerating, there is no way to determine the time at any distance when given the starting time. Using the eventual fixed speed that the car will eventually reach can give a rough approximation, but only over a long enough distance. Additionally, using the speed at any given moment cannot necessarily yield accurate results either.
In the terms of our falloff rate, this poses a problem when trying to use the inverse square formula by simply replacing the “2” with a new exponent. Taking measurements at 1 and 2 meters will give you a different exponent, or “falloff rate” than measurements at 8 and 9 meters will. Calculating a single new falloff rate and using that in the equation could result in greater inaccuracies than simply using the inverse square law. The solution is to calculate a new formula that corresponds to a power regression trend line that is based on a series of measurements at multiple distances. Luckily, we have done that for you with each of our fixtures, using distances from 1 to 10 meters, with an accuracy of 90%.
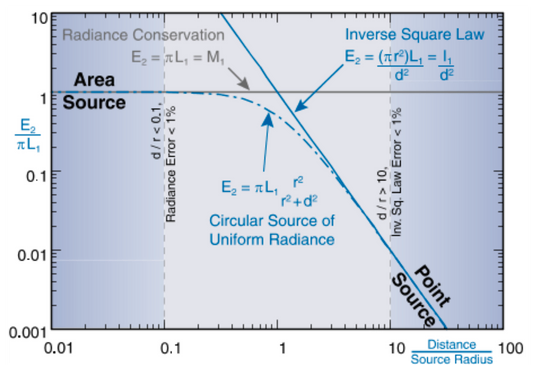

Approximation of the Inverse-Square law error, as a result of size, relative to distance. With both axis on a LOG scale, the Inverse-Square law is graphed is a constant, diagonal line. as the measurements are taken closer to the source, less of the distribution pattern is contributing to the total measurement. At a close enough point, there is no change in illuminance (radiance) when the distances change – This is represented by the constant, horizontal radiance conservation line. At a distance equal to 10x the source’s radius (5x the largest dimension), an evenly luminous, circular source will be less than 1% different than the Inverse Square law.
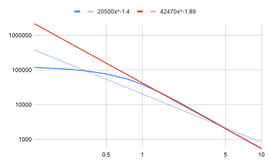

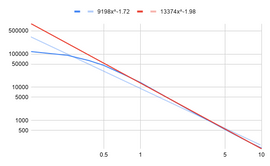

Falloff Graphs for an Astra Bi-Focus. Actual measurements follow the blue lines. 1 to 10 meters trend lines follow the red lines. While each has the same size dimensions, the Spot (left) has a different distribution pattern than the Flood (right). this results in very different falloff rates from 1 to 10 meters (Spot = 1.89, Flood = 1.98).
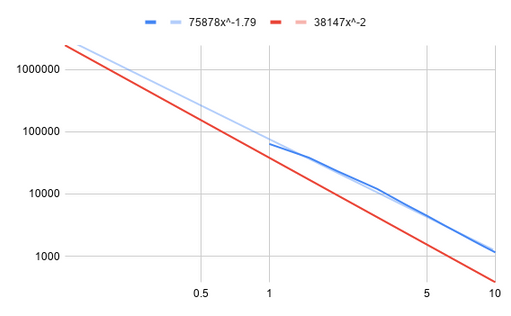

Falloff Graph for a full-spot “Junior.” The dark blue line represents actual measurements, the light blue line represents the trend line from 1-10 meters. the red line represents those measurements when distance is adjusted to the calculated “virtual point source.” At a far enough distance, the blue line will curve to meet and follow the red. However, because of the optically created distribution pattern, this distance will be much further than 5x the largest dimension.
This formula works similarly to the Inverse Square Law but with a fixed 1m Illuminance that is based off of a range of distances from 1 to 10 meters. Every fixture has an “e” number, representing a calculated approximation of energy at 1 meters, and a “regression coefficient,” representing a calculated average falloff rate that, when used with E, follows the same dynamic falloff of the fixture from 1 to 10 meters. To calculate the illuminance at any distance, use the following formula, inserting the fixture’s “e” number and regression coefficient.


Often the deviations from the Inverse-Square Law are minor and make little difference. However, there can be situations where these deviations can make or break a lighting set up and are extremely useful to understand and be able to reference in regards to choosing fixtures. To understand the complex systems at work that transform the assumed behavior of light, we encourage you to check out our in-depth look at light behavior that will be released soon.
The test took place in a 40×40 blacked-out studio with black commando cloth laid across the level, concrete floor. To conduct the test, we only took measurements along the center beam, in order to maintain consistency. Utilizing a system of levels and laser pointers, we devised a method to ensure that all readings would follow this same path. We then tested each fixture at the following distances:
0.125m 0.25m 0.375m 0.5m 0.75m 1m 1.5m 2m 3m 4m 5m 6m 7m 8m 9m 10m
We measured each fixture from the front-most part of its aperture (knowing that some would have different virtual origin points, and used necessary formulas to correct and account for this.) The meters used for this test included: Spectra Cine IV-A Professional with dome and disk, Sekonic 858-Cine, and Sekonic C-800 Spectrometer. Multiple readings were taken for reference, and all graphed data ≤ 200,000 lux comes from either the C-800 or Spectra, which had a difference of ≤ 0.2 stops from one another. Readings > 200,000 lux were taken using the 858-Cine with recessed dome, and recorded for reference and calculation purposes. Because our graphs use a maximum of 100,000 lux, specific measurements above 200,000 lux are unnecessary to display our findings and should not be used in situations in which precise measurements are necessary.



